In this tutorial, I’m going to show you how you can imitate analogue filter resonance using Phase Modulation synthesis, and offer two examples – a bass patch and a lead synth sound – that illustrate how you can use this.
Here’s a patch that I call “Grod’s Reso-Bass”:
I’m sure that you’ll recognise this type of sound, which was inspired by some old – but wonderful – analogue bass pedals that I used in the 1970s. Given that this sample was generated by Thor, it isn’t analogue of course, but it’s a great ‘virtual analogue’ sound, isn’t it? Don’t you just love that deep, resonant filter sweep? Except… this isn’t a virtual analogue patch, and that isn’t a filter sweep. Four modules generated this, and not one of them is a filter. The patch comprises just two oscillators and two envelope generators, and it’s another example of the brilliant Phase Modulation system developed by Casio in the 1980s, which has been almost universally (and unfairly) derided ever since.
We’ll start recreating this patch by making sure that everything except the Gain and Master Volume in Thor is set to ‘off’ or to zero (as appropriate), by setting the keyboard mode to Mono Retrig, and then by inserting a Phase Mod Osc in the Osc1 position. When you have done this, select the sawtooth waveform from the eight possible waves in the First slot within the oscillator, tune the pitch down to Oct=3, and make sure that the PM knob is set to zero. Next, switch on the Amp Env and push its Sustain level to maximum. If you now play a few notes you’ll hear (as I explained in tutorial #7) a sine wave, not a sawtooth wave. What’s more, you’ll obtain some nasty clicks and thunks at the start and end of each note. These are not a bug… they’re generated by the super-fast envelopes within Thor. Shown in figure 1, this is not a pleasant patch:

Figure 1: A rather unpleasant bass sound
We can refine this by modifying the Amp Env contour to eliminate the clicks, to generate a pleasing overall shape for the sound, and to control the amount of phase modulation as each note progresses. We do this by selecting suitable ADSR values and routing the envelope to the Osc1 PM Amt parameter in the modulation matrix. I find that a modulation Amount of 75 works quite nicely. (See figure 2.) This is a much nicer patch:

Figure 2: Adding some interest to the basic bass sound
If you now step through the waves offered by the First slot, you’ll find that the last three are rather unusual waveforms described in the Thor manual as…
- Saw x Sine
- Sine x Sine
- Sine x Pulse
… and by Casio as …
- Resonance I (Saw-tooth)
- Resonance II (Triangular)
- Resonance III (Trapezoid)
These were described by Casio as “resonant” because, when the PM amount is swept, each of these waveforms simulates the sound of a filter with the resonance (or “emphasis”) turned up to a high value. Some people feel that they don’t do this very convincingly but, to some extent, that’s analogue snobbery. The effect can be quite realistic and, even when it’s not, it’s very useful because it generates a new family of analogue-like sounds that are subtly different from anything you can obtain from a traditional analogue synth.
Let’s investigate these waves by increasing the Amount in the modulation matrix to 100 and placing the Resonance I waveform in the First slot. If you now play, you’ll hear sound #3 , which exhibits the distinctive character of the swept, resonant filter:
Sounds #4 and #5 demonstrate the same patch with the Resonance II and Resonance III waveforms inserted.
That second slot
Now let’s digress and look at the Second waveform slot in the PM oscillator. This does not offer the resonant waves, but allows you to select one of the five simpler, analogue-style waveforms available in the First slot. There’s nothing special about that, you may think, but what happens next is perhaps unique in synthesis. In short, the PM oscillator plays one cycle of the waveform selected in the First slot, followed by one cycle of the waveform selected in the Second slot, followed by one cycle of the waveform selected in the First slot, followed by one cycle of the waveform selected in the Second slot… and so on, ad infinitum. This allows you to construct thirty-three different waveforms, thirty of which you cannot obtain from a conventional analogue synthesiser.
Sound #6 demonstrates the tone that you obtain when you take the patch in figure 2 and insert the pulse wave in the Second slot:
(Don’t forget to re-insert the Sawtooth wave into the First slot, as before.) As well as enrichening the tone, this has reduced the pitch by an octave which, when you think about it, makes sense; if you place different waves in the First and Second slots, the wavelength of the combined waveform is now twice as long as before, so the frequency is halved.

Figure 3: Discovering the ‘Second’ slot in the PM oscillator
This patch is perfectly useable, but it’s not what we’re aiming for because we want the patch to exhibit a rather more nasal (i.e. resonant) character. We could, of course, introduce the effect of a resonant low-pass filter by inserting a resonant low-pass filter in the signal path (!) but that would be daft because the PM oscillator offers a much more efficient way to obtain this effect. By placing one of the five resonant waves in the First slot, you can superimpose the imitation of the filter sweep onto the more conventional waveform of your choice in the Second slot. Sound #7 uses Resonance III followed by a sawtooth wave:
While Sound #8 uses Resonance III followed by a square wave. (See figure 4.) These may not be identical in timbre to a VCO and a resonant LPF, but they’re surprisingly close:

Figure 4: The sound of a filter sweep – with no filter!
Doubling up
Now let’s enhance this patch further by using two detuned oscillators, with one producing roughly twice the amplitude of the other. You can set this up by adding a second Phase Mod Osc detuned to around -11, with the first tuned up by about the same amount. You then select the desired resonant waveform for the First slot in both oscillators (I have chosen Resonance I) and the desired waves in the Second slot in each. Of course, you also have to switch the second oscillator “on” in the signal path and duplicate the modulation path in the matrix so that the Amp Env is sweeping the PM in Osc1 and Osc2 by the same amount. Finally, you should adjust the Balance in the Mixer so that Osc1 is about twice as loud as Osc2. (See figure 5.) This is now starting to sound rather nice:

Figure 5: A resonant bass pedal patch
Let’s now modify this sound still further to produce the more polished example with which I started this tutorial:
This is a little more complex (see figure 6) because I have invoked a second envelope generator (the Filter Env) and two additional paths in the modulation matrix. Adding the second envelope allows me to shape the loudness and brightness of the sound independently, and I have used this to soften the attack of each note while maintaining the brightness at the start. Meanwhile, the extra modulation paths reduce the amount of Phase Modulation as I play higher up the keyboard, thus reducing the amplitudes of the upper harmonics present in higher notes relative to the amplitudes in lower ones. This is exactly what one would expect from an analogue synthesiser with limited bandwidth or a low-pass filter that is tracking at less than 100%. Finally, I have added a bit of reverb using Reason’s RV7000 and some EQ from the M-Class Equaliser. But there’s still not a low-pass filter in sight!
Figure 6: Grod’s Reso-Bass
Before leaving this topic, I’d like you to listen to a sample from a patch that I call “Real Bulls”:
This is based on the Reso-Bass patch, but without the prominent imitation of filter resonance, and I have tweaked it to make it sound similar to the most revered of all bass synths: the original Moog Taurus I pedals. Given that the synthesis behind this sound is based upon purely digital concepts, it’s an extraordinary result.
Another example of Phase Modulation synthesis
Let’s now turn our attention back to the PM knob found at the bottom of each Phase Mod Osc. As you know from last time, this determines the amount of phase modulation applied to the underlying sine wave before any additional modulation is applied, which is equivalent to setting the initial cut-off frequency of a low-pass filter.
To illustrate this, silence Osc1, increase the pitch of Osc2 to Oct = 5, and increase the PM within Osc 2 to a non-zero value; say, 68, as shown in figure 7. Now, instead of applying a positive contour as modulation, you can apply an envelope with negative polarity so that the resulting sound is similar to that of a resonant low-pass filter being rapidly closed and then slowly opened as the note progresses. Sound #11 demonstrates this nicely:
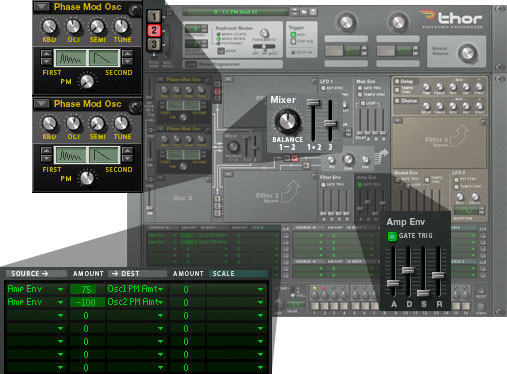
Figure 7: Imitating an inverted filter sweep
If you now un-mute Osc1 and increase its pitch to match that of Osc2, you obtain an interesting composite sound as the number of harmonics present in the Osc1 sound is swept one way, and the number of harmonics present in the Osc2 sound is swept the other:
It you then want to add further interest, there are all manner of modifications you can consider. In figure 8, I have added delayed vibrato, applied with positive polarity to Osc1 and negative polarity to Osc2. Sound #13 demonstrates this:
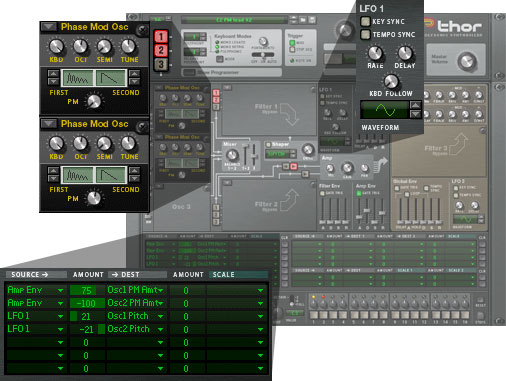
Figure 8: Creating a composite PM sound
Final touches
Now I want to add some extra body to the sound, and I do this by invoking a third Phase Mod Osc in the Osc3 slot. I have pitched this at Oct = 3, and then tuned Osc2 down by an octave and up by seven semitones to create a “Fifth” sound, as beloved of players in the 1970s and early 1980s. I have chosen to use one of the traditional analogue waveforms for Osc3 (the square wave) and again set the PM knob to a value of 68 so that the resulting tone is not too bright. Sound #14 is starting to sound like one of the large, modular synths of the 1970s, and rightly so; you cannot accurately reproduce this patch on a Minimoog, an ARP Odyssey, or any of the other integrated synths of the era:
I’m now going to apply to add a little ‘space’ to this sound, created using the delay unit within Thor itself. I have chosen a short delay time of around 30ms, with a moderate amount of relatively slow delay modulation, and a 50/50 balance between the dry and the wet signal. Finally, I’m again going to add some reverb and a bit of bass boost from the RV7000 and M-Class Equaliser. The final patch is shown in figure 9 and captured in Sound #15 . And don’t forget… there’s still not a single filter anywhere in this patch: just three ‘digital’ oscillators, an LFO and an envelope generator:

Figure 9: Triple oscillator phase modulation synthesis
So there you have it. Phase Modulation synthesis is far more than “the poor man’s FM”. Sure, it can produce sounds similar to FM synthesis, and Casio’s CZ- and VZ- series synthesisers were littered with patches that tried to compete with the DX7. But PM synthesis can also produce sounds that are very similar to analogue, subtractive synthesis. If you use PM as described here, and then invoke the filters, additional modulators, and everything else that Thor has to offer, the results can be exceptional. Learn to love Thor’s Phase Mod Osc. Phase Modulation is your friend.
Text & Music by Gordon Reid




