Last month's article in our series of Thor-centric Discovering Reason articles generated a lot of positive feedback from our readers. For those interested in vintage synths and synthesis, be sure to check out article author Gordon Reid's homepage for more goodies. When he is not explaining Thor, Gordon writes the Vintage Synth column in Sound On Sound magazine.

In the first tutorial of this series, I showed you how to create a range of important sounds using nothing more than Thor's analogue oscillators. You might think, therefore, that the next step would be to invoke things such as filters and modulators. But even without invoking Thor's more esoteric oscillator types, there's still much more that we can do with the oscillators; things such as using amplitude modulation (AM), oscillator synchronisation (sync), and pulse width modulation (PWM). In this tutorial I'm going to introduce two of these – AM and sync – and show you how you can use each of them to create one of the 'classic' families of synth sounds: the so-called 'analogue piano' patches.

What is Amplitude Modulation?

We'll start with Amplitude Modulation but, before creating a sound using it, perhaps we should ask, "what is it?".

 

To answer this, imagine that you take a continuous 'pure' tone (a sine wave) and affect its loudness (or, to use the technical terminology, modulate its amplitude) using a second sine wave with a frequency of, say, 1Hz. If you do this, you will hear the previously continuous tone get louder, then quieter, drop to silence, get louder, then quieter, drop to silence… and so on, with two silences per second. This is a very common effect, and it's called tremolo.

Let's now ask what happens if you increase the frequency of the modulation? At first, the result sounds like a faster tremolo, but as the modulator moves into the audio range, a strange thing happens… you begin to hear two distinct tones, one moving up in pitch, and the other moving down. The reason for this is straightforward to explain using a bit of high-school trigonometry, but don't worry… we'll not do the maths here. Instead, I'll just ask you to accept that, if you modulate the amplitude of one oscillator (the carrier) of frequency X using another oscillator (the modulator) of frequency Y, the result is two new signals with frequencies X+Y (the sum) and X-Y (the difference). So, if you increase Y while X remains constant, the frequency of the sum increases, while the frequency of the difference decreases. Those are the two tones that you hear:

While this may seem a bit arcane, it suggests a powerful way to obtain complex new tones using just two simple oscillators. Imagine that you have two sine wave oscillators: one with a frequency of 300Hz and the other with a frequency of 50Hz. If you combine them in an audio mixer you will obtain a sound with two frequencies present – 50Hz and 300Hz – which can be described as a fundamental and its sixth harmonic. But if you treat the first oscillator as the carrier and the second as its modulator you obtain two new frequencies, 250Hz and 350Hz, which are not harmonically related in a simple fashion. In other words, you have created a new, enharmonic, timbre.

This is not an earth-shattering result, but now imagine that you change the waveform of the carrier from a sine wave to a sawtooth wave which, as I explained in the first tutorial, contains harmonics at 300Hz, 600Hz, 900Hz… and so on. Applying the modulator to this generates partials at 250Hz and 350Hz, 550Hz and 650Hz, 850Hz and 950Hz… and up through the spectrum. This is a much more complex waveform, but it will still sound musical because all the frequencies are integer multiples of 50Hz. Next, let's change the carrier frequency from 300Hz to, say, 299Hz. This time, there are no simple relationships between the resulting partials (249Hz, 349Hz, 548Hz, 648Hz… and so on) and the result is a harsh, dissonant sound that you can not easily generate by any other means. Finally, let's change the modulator to a sawtooth wave, too… I'll leave you to work out all the frequencies present (it's a huge number) and to imagine how complex the timbre has become.

A simple example of AM

Amplitude Modulation is most commonly implemented in a device called a Ring Modulator, which you can use to create harsh sound effects, complex frequency sweeps and, when applied to a vocal signal, Dalek voices. These are all perfectly valid applications of ring modulation, but amplitude modulation can also synthesise musical tones, so I'm going to demonstrate how it can generate the waveform for an electric piano patch that will have more character than a patch based upon the basic waveforms.

 

Figure 1: The basic setup

We'll start with the basic patch from the previous tutorial, as shown in figure 1, and shape the output appropriately. We do this by reducing the sustain level in the Amplifier Envelope (Amp Env) to zero, and programming a decay of around 4s, which is a nice, natural decay for the type of sound that we want. If I play three notes using this (figure 2) it sounds like a typical single-oscillator polysynth patch:

Figure 2: Buzzy, shaped sawtooth patch

Next, we're going to make things a bit more interesting by adding a second analogue oscillator as shown in figure 3. The first remains a sawtooth with its pitch defined by Oct=3, Semi=0 and Tune=0, while the second is also a sawtooth, but with tuning of Oct=5, Semi=0 and Tune=0. If you now increase the AM slider to maximum, you'll modulate every harmonic of the carrier (at octave 3) with every harmonic of the modulator (at octave 5). But remember, you don't want to listen to the output from Osc2… you're using it only as a modulator, so you must make sure that the "2" button alongside the empty Filter 1 panel is switched off. If I play the same three notes using the modified patch, the result has a very different tone:

Figure 3: Adding a second oscillator and applying amplitude modulation

At this point, the sound is still too buzzy, so we're going to place a low-pass filter into the Filter 1 panel. You don't need to do anything too clever with this because you simply want to attenuate the higher harmonics, so set the cut-off frequency knob to around 12 o'clock, add a little resonance, and set the KBD (keyboard tracking) to around 12 o'clock. (See figure 4.) Playing the same three notes now produces sound 4:

Which is starting to sound a little like an electric piano, especially if I play something suitable from the 1970s to demonstrate this:

To illustrate the effect of the Amplitude Modulation, you should experiment with various positions for the AM FROM OSC2 slider. As you will hear, moving it the bottom to eliminate the AM removes the 'tine-y' timbre, and the result sounds much more like a basic synthesiser patch:

You can of course refine the patch in figure 4 still further, filtering the sound more carefully, using additional envelopes to shape the results more accurately, and even adding various forms of low-frequency modulation and effects to create something that could be very close to the output from a Rhodes or Wurlitzer electric piano. I've gone a little way toward this with Sound 7:

But there's no room to discuss this further. Instead, I'll leave you to experiment.

Figure 4: Static filtering of the sound in figure 3

Building a similar (perhaps better) sound using Oscillator Sync

Oscillator sync is very different from Amplitude Modulation. The easiest way to describe it is to say that when one oscillator (in this case, Osc1, the master) completes one cycle of its waveform, it resets the waveform of the "synchronised" oscillators (in this case, Osc2 and/or Osc3, the slaves). This means that the pitch of the master determines the pitch of the sound, while the pitch of the slave, if at a lower frequency, determines its timbre. Although sync can be hard to envisage, there's a good diagram in the Thor manual, so you should refer to this.

 

Oscillator sync is often used to create a distinctive type of sound, sometimes referred to as 'tearing' because it feels as if the sound is being 'torn apart'. Sound 8  (generated by the patch in figure 5) is an example of this, obtained by sync'ing Osc2 to Osc1 and then sweeping the frequency of Osc2 using one of Thor's envelope generators:

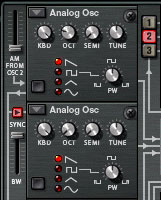
Figure 5: A typical 'sync sweep' patch

You may have noticed in the figure that the BW (bandwidth) fader beneath the Osc2 sync button is set to its maximum. Unlike the AM slider (which controls the depth of the modulation) this controls how 'hard' the synchronisation is. Some early analogue synths offered 'hard sync', which meant that the slave was reset almost instantly (i.e. with a hard edge to the resulting waveform) each time that the master completed a cycle. Others offered 'soft sync', in which the reset was less abrupt and the resulting waveform had a softer edge. Thor offers you both, and everything between, allowing you to choose how dramatic the result will be.

The example in Sound 8 is hard sync and, as you can hear, its tone changes radically as time progresses, which means that the harmonic content of the sound is different at every stage of the note. This suggests yet another type of synthesis; using sync to generate interesting new waveforms. In other words, instead of sweeping the sync'd oscillator in an arbitrary fashion, you can select the difference between the master and oscillator frequencies carefully, and use envelopes and modulators (and so on) to shape specific sounds. Again, I'll demonstrate this by synthesising an analogue piano.

We'll start with the patch in figure 4, but reduce the AM slider to zero. Now, leaving Osc1 at its previous settings (Sawtooth, Oct=3, Semi=0 and Tune=0) we'll set Osc2 to the following: Sawtooth wave, Oct=4, Semi=11 and Tune=-50. (See figure 6.) If you switch on both oscillators and play a few notes, this patch emits a rather discordant sound  with a slightly metallic flavour caused by the detuned relationship between the two oscillators:

Figure 6: Tuning the oscillators for a 'sync' piano

If you now eliminate the audio signal from Osc1, switch on the SYNC button for Osc2 and push the BW slider to its maximum, you obtain a sound that is in tune, but with a more electric-piano-like timbre:

(Indeed, sound 10 is not dissimilar to the sound that we obtained using Amplitude Modulation.)

But here's a neat trick: if you switch the audio from Osc1 back on again, you'll find that Osc1 contributes 'body' to the sound, while the sync'd Osc2 provides the overtones:

Nevertheless, the sound is still not particularly like an electric piano, and it needs a little additional filtering to shape the way that the brightness of each note changes in time.

If you look at figure 7, you'll see that I have reduced the filter's initial cut-off frequency to zero and the resonance to zero. If I play the controller keyboard with these values, I obtain silence because the filter is completely closed, so I'll make it open when I hit a note and then close over the course of a few seconds by setting the ENV amount to around 100 and setting up the Filter Envelope as shown. I'm also going to set the VEL amount to 100 or so, which means that notes played with greater velocity are brighter than those played more gently:

Suddenly… it's an electric piano!

 
Figure 7: A 'sync' piano

Of course, this just a single example of a 'sync' sound, and there are myriad other patches that take you far beyond the simple "zeeoooowww" in sound 8. Experiment with this patch, changing the oscillators' waveforms and pitch relationships and, even with such a (relatively simple) sound, you'll be surprised at how many variations you can develop. What's more, there's nothing stopping you from using amplitude modulation and sync with other oscillator types, or even at the same time! In some cases, making a change will have no audible effect – for example, it is only the frequency of the master oscillator that matters when patching with hard sync, not its waveform – but if you change the slave to another type, the effects can be radical. Unfortunately, that's a story for another day…

Text & Music by Gordon Reid